Goldbach

# 591 © Hilmar Alquiros, Philippines

Goldbach - The Gold Rush in Mathematics!

“It is comparatively easy to make clever guesses;
indeed there are theorems,
like 'Goldbach's Theorem,' which have never been proved
and which any fool could have guessed.”

Hardy (1999, p. 19)

“God made the integers; all else is the work of man.”
— L. Kronecker

Accordingly, H. Hasse listed “The dear Lord”
under “L” in the index of his book
Lectures on Number Theory! :-)

The Goldbach Conjecture is the Goldberg Variation of mathematics!

A mathematical “melody” that has been played, varied, and embellished for centuries without the final “theme” ever resolving - turns, like Bach’s musical masterpiece, endlessly and artfully around a single theme, never losing its freshness. Both require virtuosity, patience, and a touch of obsession – and both possess something timeless, almost meditative.

“This 'Nibelung treasure', the 'Rhine gold of mathematics',
will likely never be unearthed: the strong Goldbach Conjecture!
Just as the Nibelungs guarded their treasure,
number theory guards this riddle.”

Thug Catproof, USA

René Descartes already wrote:

"Every even number can be expressed as the sum of at most three primes." This proposition is similar to, but weaker than, Goldbach's conjecture.

On 7 June 1742, the Prussian mathematician Christian Goldbach wrote a letter to Leonhard Euler (letter XLIII), in which he proposed the following conjecture:

“… that every number which is composed of two numeri primi is an aggregate of as many prime numbers (including the unit) as one wishes, up to the collection of all units.” [Every integer that can be written as the sum of two primes can also be written as the sum of as many primes (including unity) as one wishes, until all terms are units].

German Original: “... dass jede Zahl,
welche aus zweyen numeris primis zusammengesetzt ist,
ein aggregatum so vieler numerorum primorum sey,
als man will (die unitatem mit dazu gerechnet),
bis auf die congeriem omnium unitatum.”

“Descartes actually discovered this before Goldbach...
but it is better that the conjecture was named for Goldbach because, mathematically speaking, Descartes was infinitely rich
and Goldbach was very poor.”
Paul Erdős

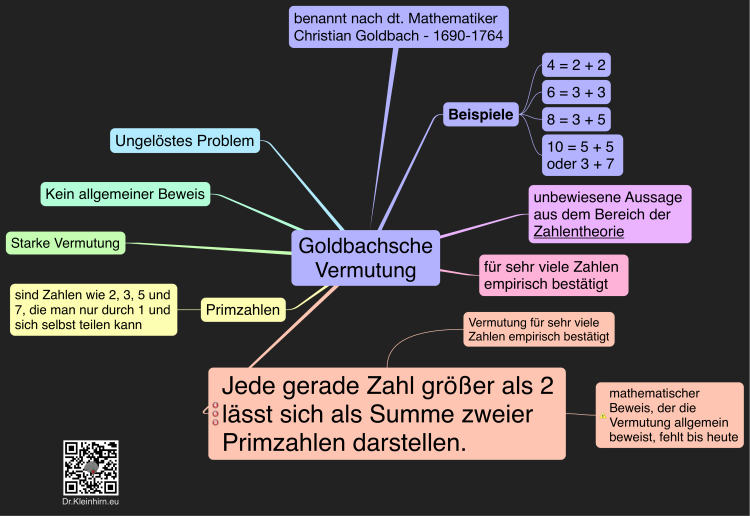
“Every even number greater than 2 is the sum of two prime numbers.”

Original (older spelling and Latin terms):

“...that every number which is composed of two prime numbers is an aggregate of as many prime numbers as one wishes (including the unit), up to the collection of all units."

Modern:

"Every number that can be written as the sum of two prime numbers can also be represented as the sum of as many prime numbers (including one) as one desires—until all terms are ones."

4 = 2 + 2

6 = 3 + 3

8 = 3 + 5

10 = 3 + 7 = 5 + 5

12 = 5 + 7

14 = 3 + 11 = 7 + 7

16 = 3 + 13 = 5 + 11

18 = 5 + 13 = 7 + 11

20 = 3 + 17 = 7 + 13

22 = 3 + 19 = 5 + 17 = 11 + 11

...

Verified up into the trillions, yet still unproven. Tested for all numbers up to 4 × 10¹⁸ – and still without a proof. Goldbach's conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even natural number greater than 2 is the sum of two prime numbers.

The weak Goldbach Conjecture: Every odd number greater than 5 can be expressed as the sum of three prime numbers. This was proven 2013 by Harald Helfgott.

The One-Million-Dollar Question

Renewed Interest in Goldbach’s Conjecture! There are probably easier ways to earn a million dollars; on the other hand, the odds are likely no worse than hitting the famous six winning lottery numbers: British publisher Faber and Faber has offered a prize of one million dollars to anyone who can confirm the truth of the so-called Goldbach Conjecture. The prize is part of a publicity campaign for a novel about this great mystery of number theory.

Wolfskehl financed his prize from his own fortune, whereas Faber insured the loss of the prize money with Lloyd’s for a five-figure sum. Perhaps for that reason, the conditions are very narrowly defined: The solution must be submitted to a mathematical journal within two years and published there within four years. Another condition hidden in the fine print breaks with every mathematical tradition: Solutions submitted only by Britons or U.S. citizens(!) will be accepted—excluding 95 percent of humanity from the prize.

Utz Thimm: SüddeutscheZeitung, 16.05.2000

That Conjecture has not been proven despite all efforts to date fuels a certain suspicion: Since the groundbreaking work of Austrian mathematician Kurt Gödel, it has been known that not every true statement in mathematics can be proven. Goldbach may therefore be right, and yet no proof will ever be found. But then again, that, too, can probably never be proven.

Goldbach’s Conjecture is less a riddle awaiting a quick solution than a musical theme, endlessly reinterpreted: even the 'Mozart of mathematics' Terence Tao seems to see no real chance to prove it. Perhaps its true appeal lies not in the proof itself, but in the centuries-long, worldwide “participation” in this grand mathematical concert.

→ German

Goldbach - Der Goldrausch der Mathematik!

""Es ist vergleichsweise einfach, kluge Vermutungen anzustellen;
tatsächlich gibt es Theoreme, wie 'Goldbachs Theorem',
die nie bewiesen wurden
und die jeder Narr hätte erraten können."

Hardy (1999, p. 19)

”Die ganzen Zahlen hat der liebe Gott geschaffen,
alles andere ist Menschenwerk.“ /
— L. Kronecker

Dementsprechend hat H. Hasse im Index seines Buches
”Vorlesungen über Zahlentheorie¨
unter ‘L‘ den ”Lieben Gott“ aufgeführt! :-)

Die Goldbach-Vermutung ist die Goldberg-Variation der Mathematik!

Eine mathematische „Melodie“, die seit Jahrhunderten gespielt, variiert und ausgeschmückt wird, ohne dass sich das finale „Thema“ je auflöst – sie kreist, wie Bachs musikalisches Meisterwerk, endlos und kunstvoll um ein einziges Thema, ohne jemals ihre Frische zu verlieren. Beide erfordern Virtuosität, Geduld und eine Prise Besessenheit – und beide besitzen etwas Zeitloses, fast Meditatives.

Thug Catproof, USA

René Descartes schrieb: „Jede gerade Zahl kann als Summe von höchstens drei Primzahlen dargestellt werden.“ Dieser Satz ist der Goldbachschen Vermutung ähnlich, aber schwächer.

Am 7. Juni 1742 schrieb Christian Goldbach an Leonhard Euler einen Brief (Nr. XLIII), der – trotz seiner knappen Form – das mathematische Denken bis heute beschäftigt. Dort steht in lateinischer Syntax, aber mit ewiger Spannung:

“Jede Zahl, die sich als Summe zweier Primzahlen darstellen lässt, kann auch als Summe von so vielen Primzahlen (einschließlich der Eins) dargestellt werden, wie man möchte – bis alle Glieder Einsen sind.”

„Descartes entdeckte dies tatsächlich vor Goldbach…
aber es ist besser, dass die Vermutung nach Goldbach benannt wurde,
denn mathematisch gesehen war Descartes unendlich reich
und Goldbach sehr arm.“ :-)

Paul Erdős

Die starke Goldbachsche Vermutung:

Jede gerade Zahl größer als 2 ist die Summe zweier Primzahlen.

Original (Alte Schreibweisen und Latein):

„... dass jede Zahl, welche aus zweyen numeris primis zusammengesetzt ist, ein aggregatum so vieler numerorum primorum sey, als man will (die unitatem mit dazu gerechnet), bis auf die congeriem omnium unitatum.“
= „… dass jede Zahl, welche aus zwei numeri primi zusammengesetzt ist, ein Aggregat so vieler numerorum primorum ist, wie man will (eins eingeschlossen), bis zur Menge aller Einsen.“

Modern:

= Jede Zahl, die sich als Summe zweier Primzahlen schreiben lässt, kann auch als Summe von so vielen Primzahlen (einschließlich der Eins) dargestellt werden, wie man möchte – bis alle Glieder Einsen sind.

4 = 2 + 2

6 = 3 + 3

8 = 3 + 5

10 = 3 + 7 = 5 + 5

12 = 5 + 7

14 = 3 + 11 = 7 + 7

16 = 3 + 13 = 5 + 11

18 = 5 + 13 = 7 + 11

20 = 3 + 17 = 7 + 13

22 = 3 + 19 = 5 + 17 = 11 + 11

...

Verifiziert bis in die Billionen, doch immer noch unbewiesen. Getestet für alle Zahlen bis 4 × 10¹⁸ – und immer noch ohne Beweis. Die Goldbachsche Vermutung ist eines der ältesten und bekanntesten ungelösten Probleme in der Zahlentheorie und der gesamten Mathematik. Sie besagt, dass jede gerade natürliche Zahl größer als 2 die Summe zweier Primzahlen ist. Man könnte fast meinen...

Die schwache Goldbach-Vermutung: Jede ungerade Zahl größer als 5 kann als Summe von drei Primzahlen ausgedrückt werden. Diese wurde 2013 von Harald Helfgott bewiesen.

Die Eine-Million-Dollar-Frage.

Erneutes Interesse an der Goldbachschen Vermutung! Es gibt wahrscheinlich leichtere Wege, eine Million Dollar zu verdienen; andererseits sind die Chancen vermutlich nicht schlechter als beim berühmten Sechser im Lotto: Der britische Verlag Faber and Faber hatte eine Prämie von einer Million Dollar für denjenigen ausgelobt, der die Wahrheit der sogenannten Goldbachschen Vermutung bestätigen kann. Der Preis ist Teil einer Werbekampagne für einen Roman über dieses große Rätsel der Zahlentheorie. Aber...

Wolfskehl finanzierte seinen Preis aus eigenem Vermögen, während Faber den Verlust des Preisgeldes mit einer fünfstelligen Summe bei Lloyd’s versicherte. Vielleicht deshalb sind die Bedingungen sehr eng gefasst: Die Lösung muss innerhalb von zwei Jahren bei einer mathematischen Fachzeitschrift eingereicht und dort innerhalb von vier Jahren veröffentlicht werden. Eine weitere Bedingung im Kleingedruckten bricht mit jeder mathematischen Tradition: Nur Einsendungen von Briten oder US-Amerikanern(!) werden akzeptiert – 95 Prozent der Menschheit sind vom Preis ausgeschlossen.

Utz Thimm: Süddeutsche Zeitung, 16.05.2000

Dass die Goldbachsche Vermutung trotz aller bisherigen Anstrengungen nicht bewiesen wurde, nährt einen gewissen Verdacht: Seit der bahnbrechenden Arbeit des österreichischen Mathematikers Kurt Gödel weiß man, dass nicht jeder wahre Satz der Mathematik auch beweisbar ist. Goldbach könnte also recht haben – und dennoch wird nie ein Beweis gefunden. Aber auch das wiederum lässt sich vermutlich nie beweisen!

Goldbachs Vermutung ist weniger ein Rätsel, das auf eine schnelle Lösung wartet, als vielmehr ein musikalisches Thema, das endlos neu interpretiert wird: Sogar der „Mozart der Mathematik“, Terence Tao, scheint keine wirkliche Chance zu sehen, sie zu beweisen. Vielleicht liegt ihre wahre Anziehungskraft nicht im Beweis selbst, sondern in der jahrhundertelangen, weltweiten „Teilnahme“ an diesem großen mathematischen Konzert.