174WhiteMagic

White Magic

von Hilmar Ebert, Aachen,

und Hans-Peter Reich, Kaarst

Neben der SPASS-Stellung (siehe Hilmar Ebert, Die Schwalbe II/1995, weiterführende Literaturverweise ebendort) existieren natürlich auch Aufgaben mit der weißen Partieanfangsstellung, die ihren eigenen Reiz ausstrahlen. Im folgenden sehen Sie eine Zusammenstellung dieser Aufgabengattung, die natürlich wieder eigene Kompositionen anregen soll.

Sam Loyd

Chess Monthly 1858

#3 (16+1)

1.Sh3?/1.d3? Kh5!; 1.e3(e4)? Kg5! (h.e.)

1.d4! Kh5 2.Dd3 Kh4(g4) 3.Dh3#

1....Kg4 2.e4+ Kh4 3.g3#

Anmerkung:

Max Lange, Schachzeitung 1858, S. 232, Nr. II analog farbvertauscht (!):

„Zur Revanche rief darauf Weiss: „Ich gebe Dir aber alle Figuren vor, wenn ich nur meinen König, statt auf seinem Standfelde e1, dort, wo es mir beliebt, aufstellen dürfte; dann wette ich, dass Du nicht weniger Züge gebrauchest“. Und nachdem Schwarz seine sämmtlichen Figuren in Schlachtordnung gebracht hatte, stellte Weiss in kühnem Selbstgefühle seinen König auf ein Feld, wo er gerade in möglichst kurzer Zügezahl und zwar viermal schneller, als er gedacht hatte, matt gesetzt wurde.

Auf welches Feld stellte Weiss seinen König, so dass er in kürzester Zügezahl durch die in voller Aufstellung stehende Gegenpartei matt gemacht werden konnte?“

Karl Fabel

Schwalbe XII/1942

#5 (16+1)

1.c3? Kb5!; 1.e3(4)? Ka5! (h.e.)

1.c4+! Kb4(!) 2.d4!! Ka5 3.Db3 Ka6 4.Db8 Ka5 5.Db5#

2...Kc4: 3.e4+ Kb4 4.Ld2#

1...Ka5 2.Db3 Ka6 3.Db8 Ka5 4.Db5#

1.c3? Kb5!

1.e3(e4)? Ka5! (h.e.)

1…c4+ (h.e.?) 1…Kc4!1.d2!! Ka5 1…Ddb8 Ka5 1.Da8 Ka5 1…Dd5# Schlüssel;

aber ein zusätzliches Märchenelement (Hans-Peter Reich, Urdruck, §4, CousCousCirce) verkürzt Fabels Aufgabe um einen Zug, da Selbstdeckungen beschleunigt zum Ziel führen:

1.c4! 1…Ka5 2.Db3 Ka6 3.Db8 Ka5 4.Dd8#,

1…Kc5 2.Dd4+ Ke5 3.De6+ Kd4 4.Dd5/Sf3#,

3. — Kb4 4.Db5#

Max Lange

Schachzeitung 1858

Auf welchem Feld maximales #n?! (16+0)

♚ + ♛ + ♟= „kürzestes Matt?“

(Schachzeitung 1858, S. 232 (Fußnote 7, S.12) plus sKf4, sDf5: 1.d4+ Kg4 (Ke4 2.Sc3!) 2.e4+ Df3 3.Df3+ 4.Dh3# (1.d3? Ke5!))

„Verschiedene Denkübungen solcher Art hat der Autor in der Schachzeitung von 1858, S. 232 mitgeteilt, z. B.: Die Aufgabe, König und Dame so zu stellen, daß jener durch die in voller Aufstellung stehende Gegenpartei in kürzester Zugzahl matt gesetzt werde.

Die Felder sind f4 und f5, die Züge 1.d4 Ke4 (falls Ke5 4.2.Sc3?) 2.e4+ Df3 3.Df3+ nebst 4.Dh3#.“ [4.3# Dual]

Originaltext: „Diese Spiele scheinen Weiss und Schwarz allmählich (!) zu gefallen. Ein andermal rief Weiss, nachdem er Schwarz ruhig seine Figuren hatte aufbauen lassen: ‚Ich beginne mit König und Dame und gestatte Dir sogar, die Felder ihrer Aufstellung vorzuschreiben, parity (!) aber, dass Du meine beiden Figuren nicht so aufzustellen vermagst, um in kürzester Zugzahl matt zu machen.‘ Schwarz nahm die Wette an und fand glücklich die richtigen Felder. Welche sind diese, und wie viel Züge, welche sind die notwendigen Züge?“

In Gik, Schach + Mathematik, 1983, taucht zum ersten Mal die Frage auf, auf welchem Feld der schwarze König eingesetzt werden muß, um ein maximales #n zu erzwingen. Antworten:

e4: 7 Züge (Gik, S.126) – wie?! (h.e.)
I) 1.Sh3!; II) 1.Sc3! (z. B. Kd5 2.e4 Ke5 3.Dg4+ Ke7 4.Dg7+ Kd6 5.d4 Kc6 6.Lf4 Kb6 7.De7# u. v. m.!)
d4: 6 Züge, 3 dualfreie Varianten, z. B.:
1.e4! Ke5 2.Dg4 Kd6 3.Dg7 Kc6(c6) 4.d4 Kd6 5.Lf4+ Kc6 6.Dc7#

In Computerschach und Spiele XII/1994, S. 40 erschien dann die vollständige Analyse, mit dem Ergebnis, daß auf allen Feldern das Matt in 6 Zügen zu schaffen ist, Ausnahmen: h4 = 3 Züge (Loyd), a4 = 5 Züge (Fabel) und e4 = 7 Züge (Rekord!)

Henry E. Dudeney & William A. Shinkman

Leeds Mercury Supplement, 1895

[zit. n. Dickins, Märchenschach, S.92]

Stellung nach dem 16. Zug von Weiß. Wie verlief die Partie? (16+1)

Dudeney, Henry Ernest (1857-1930): 1.Sc3 d5 2.Sd5: Sc6 3.Se7: g5 4.Sc8: Sf6 5.Sa7: Se4 6.Sc6: Sc3 7.Sd8: Tg8 8.Sf7: Tg6 9.Sg5: Te6 10.Sh7: Sb1 11.Sf8: Ta3 12.Sce6 b5 13.Sc7:+ Kf7 14.Sb5: Kg6 15.Sa3: Kg5 16.Sb1: Kh4 (Gik, Schach + Mathematik, S. 126)

Fabel, Karl Schwalbe XII/1942: 1.Sa3 (c3) b5 2.Sb5: Sf6 3.Sa7: Se4 4.Sc8: Sc3 5.Se7: c6 6.Sc6:! Sb1 7.Sb8: Ta3 8.Sd7: g5 9.Sf8: Dd6 10.Sh7: Kd7 11.Sg5: Th4 (c8) 12.Sf7: Tc4 13.Sd6: Kc6 14.Sc4: Kb5 15.Sa3:+ Ka4 16.Sb1:. Die Stellungen nach dem 8. bis 10. Zug entstehen wohl zwangsläufig?!

Gik, J. : 1.Sc3 d5 2.Sd5: g6(!) 3.Se7 b5 4.Sg6: a6 5.Sh8: Ld7 6.Sf7: Dg5 7.Sg5: Sf6 8.Sh7: Se4 9.Sf8: Sc3 10.Sd7: Sb1 11.Sb8: Kf7 12.Sa6: Kg6 13.Se7: Kh5 14.Sb5: Ta3 15.Sa3: Kh4 16.Sb1: (Gik, Schach + Mathematik, S. 126)

Ergänzungen [zit. n. Dickins, Märchenschach, S.92]

Thompson, W. H. (British Chess Magazine, XII/1934): mit zweifachem Schlagen auf nur einem Feld;

Cross, W. (British Chess Magazine, XII/1935): Doppelbesuch des Springers auf drei Feldern;

Deane, A. M. (British Chess Magazine, IX/1898): 15 ½ Züge! [Fairy Chess Review 3/16 S.117 und U.T. 135a, = zit. n. Dickins]

Dudeney, Henry Ernest (zitiert in Dickins, Märchenschach, S.92):

1.Sc3 d5 2.Sd5 Sc6 3.S e7 g5 4.Sc8 5.Sc f5 5…a7 Se4 6.Sc5 6…b5 7.3 5.d8 T g8 8…5 3.Tg6 9.5 9…T g6 10.Se5 6.5 b5 11.Lb8 Kb6 12.5 S…6 15.Lh6 Kh4 (Gik, Schach + Mathematik, S.126)

C. Becker (Karl)

F307, The Problemist VII–IX/1975

„♚ für korrektes h=2“ (16+0)

sKc6, → 1.Kd5 e3 2.Ke4 Dh5=

Hilmar Ebert nach N. Geissler

Urdruck

Zuglängstes und zugkürzestes korrektes

a) ser–#n

b) ser–an

für welche sK-Felder? (16+0)

Die Stellungen nach dem 6. bzw. 8. Zug entstehen wohl zwanglläufig?!(Karl Fabel, Die Schwalbe XII/1942)

Shinkman, W. A.:

1.Sc3 d5 2.S:d5 g6(!) 3.Se7 b5 6.S:g6 a6 5.S:h8 Ld7 6.S:f7 Dg5 7.S:g5 S f6 8.S:h7 Se4 9.S:f8 Sc3 10.S:d7 Sb1 11.S:b8 Kf7 12.S:a6 Kg6 13.S:e7 Kh5 14.S:b5 Ta3 15.S:a3 Kb4 16.S:b1 (Gik, Schach + Mathematik, S.126)

Ergänzungen [zit. in Dickins, Märchenschach, S.126]:

- Thompson, W. H. (British Chess Magazine, XII/1934):

mit zweifachem Schlagen auf nur einem Feld;

- Cross, W. (British Chess Magazine, XII/1935):

Doppelbesuch des Springers auf drei Feldern.

- Deane, A. M. (British Chess Magazine, IX/1898): 15 1/2 Züge!

(Fairy Chess Review 3/16 S.117 und U. T. 135a, = zit. n. Dickins)

a) sKd4? – 1.e4 2.e5 3.Dd5#, sKh7! – 1.e3! 2.Df3 3.Df8 4.Ld4#

– Doppel- und Einzelschritt des e-Bauern als Schlüsselzüge!

Die einzigen dualfreien Königsfelder.

b) sKe4? – 1.e3! 2.Dh5=, sKg4! – 1.d4! 2.Dd3 3.Dh7=

– Die einzigen dualfreien Königsfelder.

Andere dualfreie Königsfelder gibt es überhaupt nicht, so daß die kürzeren Zugfolgen als „Verführungen“ der zuglängsten Königsfelder gelten können.

Die Partieforderungen sind erschienen als Geissler, N. (10/11, Problemkiste VIII/1994)

7 Norbert Geissler

9. Problemkiste VIII/1994

ser–#3 KöKo (16+1)

b) ♚f5→c5

a) 1.e4! 2.d4 3.Dg4#;

b) 1.d4! 2.e4 3.b4#

8 Norbert Geissler

7. Problemkiste VIII/1994

a) ser–Ze8 in 3, b) ser–Zg8 in 3 (16+1)

a) 1.c4! 2.Da4 3.Dd8 Z; b) 1.c3! 2.Dg8 Z

9 Norbert Geissler

8. Problemkiste VIII/1994

a) ser–Za6 in 3, b) ser–Za7 in 3, c) ser–Zc7 in 3, d) ser–Zd8 in 3 (16+1)

a) 1.d4! 2.e5 3.a3!

b) 1.Sc2! 2.b5 3.a7 Z;

c) 1.b4! 2.g5 3.Ld8 Z

10 Norbert Geissler

6. Problemkiste VIII/1994

a) ser–Za8 in 3 b) ser–Zh6 in 3. 2 Lösungen (16+1)

a) 1.g4! 2.Lg2 3.La8 Z; II) 1.c4! 2.Da4 3.Dd8 Z;

b) 1.a4! 2.h5 3.b6 Z;
c) 1.Dh6 Z!

11 Theodor Steudel

342, 32er X/1995

ser–h=9 (16+2)

1.Kc4! 5.b5! b2 c:c5 b:s 7.Sc8 5.e2 9.Kd4 Dh4

12 Hilmar Ebert, Jörg Kuhlmann, Hans-Peter Reich

Urdruck

#4 (16+1)

Cavalier Majeur, Circe, 2 Lösungen

1.d3! 7.Kf5! 1.e4+ 7.Ke5! b… 7.Kh5 2.h4 Kg4 3.e5#

Hilmar Ebert, Jörg Kuhlmann, Hans-Peter Reich

Urdruck

#3 Cavalier Majeur (16+1)

a) Kürzestzüger, 1.1, b) Längstzüger, 3.1…

a) 1.h4! Kf4! 2.e4 K:e4 3.Dg4#;

b) I) 1.d4! Kf5(!) 2.Dd3+Ke6 3.Db6#

II) 1.e3+! Kf5 2.Db6 Ke6(!) 3.Dg6#;

III) 1.e7! 2.e8=T 1.Kh5 2.h4 Kg4 3.e5#

Hans-Peter Reich

Urdruck

ser–#3 Cavalier Majeur (16+1)

1.c4! 2.Db3 3.Db6#

1.c3? verstellt Nachtreiterlinie!

Norbert Geissler

3507. Problemkiste VIII/1994

a) ser–Zb6 in 3, b) ser–Zd7 in 3, 3 Lösungen (16+1)

a) 1.b4 2.a2 3.b6 Z; a2) 1.Sa3 2.Sc4 3.Sb6 Z;

b) I. 1.d3 2.Le3 3.Lb6 Z;

II. 1.g2 2.Lh3 3.Ld7 Z;

III. 1.Sf3 2.Se5 3.Sd7 Z

Schöne Eindeutigkeit in den 6 Phasen!

Bengt Ingre

The Problemist VI/1988, S. 367

Kriegsspiel. W’s best move? (16+0)

1.Sh3! Bl. may threaten mate on f2!

George Jelliss

Suomen Tehtäväniekat 1987

4. Preis

Kürzestes „Patt“? (Eigenpatt!). Wie viele (unterschiedliche) Schlußpositionen? Gitterschach (16+0)

zitiert in The Problemist III/1988, S.405)

Eine Schlussposition! -

1.d3 2.Lh6 3.Ld2 4.e3 5.g3 6.Le2 7.Lf3 8.Le2 9.f3 10.a3 11.b3 12.c3 13.h3

Min-13 – a3,b3,c3,h3; 13 × 12 × 11 × 10 = 17.160 Wege;

(d3–Lh6–Ld2–e3) und g3,Lg2-Lf3 vor Le2-f3!;

Diese 9 Züge = 35 gegenseitige Folgen.

Lc1 4 × (e3,f4,5,b6) ergibt × 2 (Symmetrie) = 17.160 × 35 × 4 × 2 = 4.804.800.

A. Wijker nach W. H. Thompson

Probleemblad XII/1946, S. 83

Letzter Zug? (16+1)

Lösung Het zet, März 1947.

„Deze kluit bleek niet gemakkelijk te wezen. Er kwamen vijf oplossingen binnen, waarvan geen enkele de oplossing van den heer Wijker: („Dieser Brocken erwies sich als nicht leicht. Es gingen fünf Lösungen ein, von denen keine an die Lösung von Herrn Wijker heranreichte.“)

1.Sc3 d5 2.Sd5 g6 3.Se7 Ld7 4.Sg6? Dg5 5.Sb5 6.Sf7 b7 5…7.Sg5 6.S h7 Se4 9.S8 c6 7… b3! 2.Sc e6 11.S:b8 Ke7 12.S a6! Kd6 13.Se c7 Ke5 14.b5 5: Ta3 15.S a3 Kd4 16.S:b1 „Wit dus de laatste zet doen en wel als volgt:“ („Weiß muss also den letzten Zug machen, und zwar wie folgt:“)

1.Sc3 5 2.b5 5: 6.5 7… Sc3 5.S5 c7 6.c6 5: Sb1 7.5 b8 Ta3 8.S8 d7 5.98 Dd6 10…Sb7 Kd7 11.S5 9: S e6 12.S f7 13…S d6 14.c4 15…Ta3 16.e4 K b5 15…5 Sa3! Ka4 16.Sb1

„Hij heeft hiermee de prijs zeker wel verdiend. Een knappe prestatie! Vermelding verdient nog de heer F. C. Laas, die eveneens als heer Wijker slechts de stelling op de 16de zet te bereiken, waarbij echter de rondrit met het Koningspaard werd gemaakt. De overige drie oplossers deden er langer over.“ („Damit hat er den Preis auf jeden Fall verdient. Eine beeindruckende Leistung! Erwähnung verdient noch Herr F. C. Laas, der – ebenso wie Herr Wijker – die Stellung ebenfalls erst im 16. Zug erreichte, dabei aber den Rundlauf mit dem Königsspringer ausführte. Die übrigen drei Löser benötigten länger.“

)

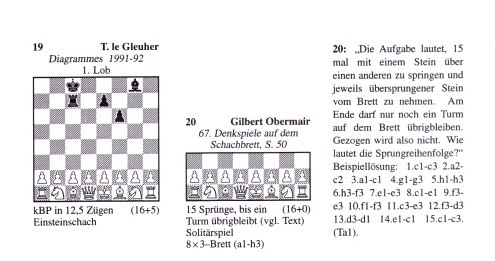
T. le Gleuher

Diagrammes 1991–92

1. Lob

kBP in 12,5 Zügen. Einsteinschach (16+5)

zit. A1162 – Phenix 29, V/1995 S. 2747.

1.e3 h5 2.D h5 4.De5 3.Dd5 Th5L 4.D b7: Ld1 5.De7: Lg45 (6.D:a7D e7T 7.D b8+ 7.Df8 5 9.D g7 5f6=

10.D g4 Tg8L 11.D d1 14 12.e f4 5 Tc8 13.Se2=B.

Gilbert Obermair

67. Denkspiele auf dem Schachbrett, S. 50

15 Sprünge, bis ein Turm übrigbleibt (vgl. Text). Solitärspiel.

8 × 3–Brett (a1–h3) (16+0)

Die Aufgabe lautet, 15 mal mit einem Stein über einen anderen zu springen und jeweils übersprungenen Stein vom Brett zu nehmen. Am Ende darf nur noch ein Turm auf dem Brett übrigbleiben. Gezogen wird also nicht. Wie lautet die Sprungreihenfolge?

Beispiellösung:

1.c1–c3 2.a2–c2 3.a1–c1 4.g1–g3 5.h1–h36.h3–f3 7.f3–f1 8.f1–h1 9.c3–c1 10.f1–f3 11.c3–e3 12.f3–f1 13.d3–d1 14.c1–c3 15.c1–c3. (Tal.)

----------------------------------------------------------------------

Nachträge:

E. B. Cook, zit.: 21. American Chess Nuts 1868 S. 400, C-, s=16

„Self-stale in the sixteenth move - Black not to stand finally on his royal or second rank.“ („American Chess Nuts“ = Buch von Cook, Henry & Gilberg)

Pal Benkö, Sakkelét 1987, w-16; sKh4, sBd7, shs=8 , C-,

Zit. Zaszlonk 9/1992/3. 1.d5 2.d4 3.d3 4.de2: 5.ef1:S 6.Sd2 ??.Sf1(3) Sh2:=