
hilmar ebert, aachen
Faschingsschach 2000 ...
Sensation: Mensch löst Schachaufgabe 16 mal „schneller“ als Computer!
Da die Zeit bekanntlich immer schnelllebiger zu werden beliebt, liegt es nahe, auch das Lösen von Schachaufgaben über die radikale Verkürzug der geforderten Zügezahlen zu beschleunigen. Zeitvergeudung, Matt in drei oder noch mehr Zügen zu lösen– dafür gibt es doch Computer! Tele-Tipp 1.1.2000[1] Computer benötigen hier 4 volle Züge, also das Sechzehnfache der menschlichen Zügezahl, ein schier unüberbietbarer Rekord!?
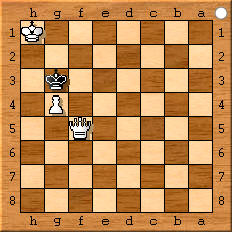
Computer: Matt in 4! 1.Dd5?/1.Dc7+? Ka5!; 1.Dd4+? (Kb5:?/Kc7?) aber: 1...Ka5! Darum:
1.Kb8!? Ka5 2.Kc8! Kb6 3.Db4 Ka7 4.Da5# - Na ja, Preisniveau erreicht diese schnöde Lösung sowieso nicht.
Mensch: Matt in ¼! Die wesentlich geistvollere humanoide Lösung! Schwarz hatte natürlich zuletzt a7-a5 gezogen, das dürfen wir (allerdings nur an Fasching und an Silvester!) unterstellen. Der schwarze Bauer a5 wurde bereits entfernt (e.p.-Schlag) = ein halber Zug; der Bauer führt nun von seinem nächsten halben Zug (b5-a6) nur die Hälfte aus, landet also auf dem Schnittpunkt aus a/b und 5/6 = ein Viertelzug, von wo aus er fröhlich mattsetzt, von der Dame sichtlich gedeckt. Überdies ein sogenanntes Idealmatt, da alle Steine am Matt beteiligt sind und jedes Fluchtfeld aus nur einem Grunde verwehrt ist, somit problemschachästhetisch begründet!
P.S. In Hilfsmatt-üblicher Zählung (der weiße Mattzug als Teil eines Zugpaares = Halbzug) ist hier bereits das (Hilfs-) Matt in einem Achtelzug erreicht, drum setzt der Autor an dieser Stelle ein Flasche Champagner aus für die erste korrekte Darstellung eines Matt in einem Sechzehntelzug ...
[1] Auszug aus einem Silvesterschach-Artikel
wKa8, wDc4, wBb5 - sKb6: Mate in a quarter move (!!!)
hilmar ebert, aachen
Mardi Gras Chess 2000...
Sensation: Man solves chess problem 16 times "faster" than computer!
As it is well known that time is becoming more and more fast-moving, it is obvious to speed up the solution of chess problems by radically shortening the required number of moves. Waste of time, solving Mate in three or even more moves - that's what computers are for! Tele-Tip 1.1.2000[1] Computers need 4 full moves, i.e. sixteen times the number of human moves, an almost unbeatable record!
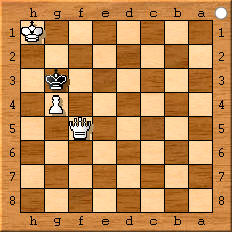
Computer: Matt in 4! 1.Dd5?/1.Dc7+? Ka5!; 1.Dd4+? (Kb5:?/Kc7?) but: 1...Ka5! That's why:
1.Kb8!? Ka5 2.Kc8! Kb6 3.Db4 Ka7 4.Da5# - Well, price level does not reach this disdainful solution anyway.
Man: Matt in ¼! The much more ingenious humanoid solution! Of course Black had drawn a7-a5 last, we may assume that (but only at carnival and on New Year's Eve!). The Black pawn a5 has already been removed (e.p.-hit) = half a move; the pawn now only moves half of its next half move (b5-a6), thus landing at the intersection of a/b and 5/6 = a quarter move, from where it happily mates, visibly covered by the queen. Moreover, this is a so-called ideal checkmate, since all the pieces are involved in the checkmate and each escape field is denied for only one reason, thus justified in terms of problem chess aesthetics!
P.S. In the usual auxiliary mate count (the white mate move as part of a pair of moves = half move), the (auxiliary) mate is already reached in an eighth move, so the author exposes a bottle of champagne at this point for the first correct representation of a mate in a sixteenth move ...
1] Excerpt from an article on New Year's chess
© by Hilmar Alquiros, The Philippines Impressum Datenschutzerklärung