
# 596:
©
Hilmar Alquiros,
Philippines

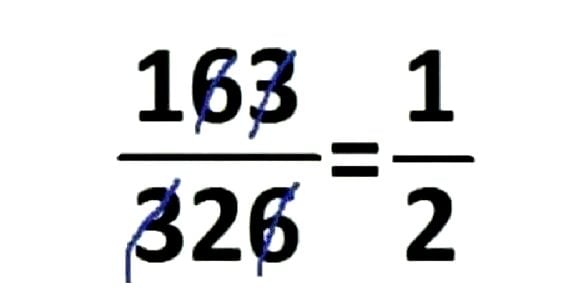
FUN FRACTS!
Anomalous Cancelling Fractions

→ German
Sometimes in mathematics you are allowed to do something that is usually forbidden: you simply cross out identical digits in numerator and denominator — and the fraction remains valid!
Already in the early problems of Project Euler (Problem 33) this phenomenon appears. There are exactly four non-trivial two-digit examples (cf. Project Euler 33, R solution on R-Bloggers):
16/64 → 1/4 (cancel the 6)
19/95 → 1/5 (cancel the 9)
26/65 → 2/5 (cancel the 6)
49/98 → 4/8 = 1/2 (cancel the 9)
In the literature, they are called digit-cancelling fractions or anomalous cancelling fractions.
"Euler Problem 33"
| # | a/b | off | c/d | :x |
| 1 | 16/64 | 6 | =1/4 | :16 |
| 2 | 19/95 | 9 | =1/5 | :19 |
| 3 | 26/65 | 6 | =2/5 | :13 |
| 4 | 49/98 | 9 | =1/2 | :49 |
Extending the search to three-digit numbers and requiring that two digits must be cancelled (and not more than one digit "0") is used produces the truly surprising examples — we call them here the Aesthetic Fun Fracts.
For example:
124/217 → 4/7 (cancel 1+2)
163/326 → 1/2 (cancel 3+6)
316/632 → 1/2 (cancel 3+6)
455/546 → 5/6 (cancel 4+5)
499/998 → 1/2 (cancel 9+9)
Altogether I found 30 such elegant cases in the 3-digit range:
Non-trivial Anomalous Cancelling Fractions >100
| # | a/b | off | c/d | :x |
| 1 | 124/217 | 1 + 2 | =4/7 | :31 |
| 2 | 127/762 | 2 + 7 | =1/6 | :127 |
| 3 | 138/184 | 1 + 8 | =3/4 | :46 |
| 4 | 139/973 | 3 + 9 | =1/7 | :139 |
| 5 | 145/435 | 4 + 5 | =1/3 | :145 |
| 6 | 148/185 | 1 + 8 | =4/5 | :37 |
| 7 | 160/640 | 0 + 6 | =1/4 | :160 |
| 8 | 163/326 | 3 + 6 | =1/2 | :163 |
| 9 | 166/664 | 6 + 6 | =1/4 | :166 |
| 10 | 182/819 | 1 + 8 | =2/9 | :91 |
| 11 | 187/748 | 7 + 8 | =1/4 | :187 |
| 12 | 190/950 | 9 + 0 | =1/5 | :190 |
| 13 | 199/995 | 9 + 9 | =1/5 | :199 |
| 14 | 218/981 | 1 + 8 | =2/9 | :109 |
| 15 | 244/427 | 2 + 4 | =4/7 | :61 |
| 16 | 260/650 | 0 + 6 | =2/5 | :130 |
| 17 | 266/665 | 6 + 6 | =2/5 | :133 |
| 18 | 273/728 | 2 + 7 | =3/8 | :91 |
| 19 | 316/632 | 3 + 6 | =1/2 | :316 |
| 20 | 327/872 | 2 + 7 | =3/8 | :109 |
| 21 | 364/637 | 3 + 6 | =4/7 | :91 |
| 22 | 412/721 | 1 + 2 | =4/7 | :103 |
| 23 | 424/742 | 2 + 4 | =4/7 | :106 |
| 24 | 436/763 | 3 + 6 | =4/7 | :109 |
| 25 | 448/784 | 4 + 8 | =4/7 | :112 |
| 26 | 455/546 | 4 + 5 | =5/6 | :91 |
| 27 | 484/847 | 4 + 8 | =4/7 | :121 |
| 28 | 490/980 | 9 + 0 | =1/2 | :490 |
| 29 | 499/998 | 9 + 9 | =1/2 | :499 |
| 30 | 545/654 | 5 + 4 | =5/6 | :109 |
The literature (cf. Boas 1979, and Wolfram MathWorld: Anomalous Cancellation) shows that in the 4-digit range there are many such fractions — in fact 1851 in total. However, many of these are “trivial” (often only zeros being cancelled).
Some of the first non-trivial examples (from MathWorld/Wolfram):
| # | a/b | off | c/d |
| A | 1016/4064 | 6 | =101/404 |
| B | 1019/5095 | 0 + 9 | =11/ 55 |
They demonstrate that the phenomenon is not limited to small numbers — but the really beautiful, “humanly surprising” examples become rarer.
L. Boas (1979): Curious Cancelling Fractions
Project Euler Problem 33: Digit Cancelling Fractions
Wolfram MathWorld: Anomalous Cancellation
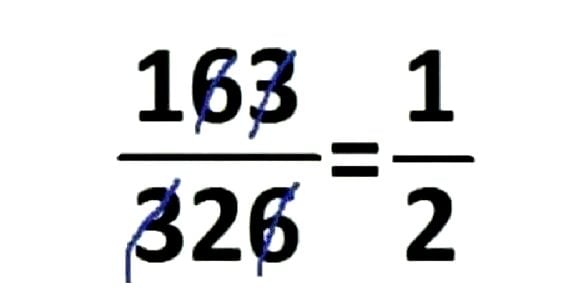
FUN FRACTS!
Kuriose Kürzungsbrüche
→ English
Manchmal darf man in der Mathematik etwas tun, das eigentlich streng verboten ist: man streicht einfach gleiche Ziffern in Zähler und Nenner – und der Bruch bleibt trotzdem richtig!
Schon in den frühen Aufgaben von Project Euler (Problem 33) taucht das Phänomen auf. Es gibt genau vier nicht-triviale zweistellige Beispiele (vgl. Euler Project 33, R-Lösung auf R-Bloggers):
16/64 → 1/4 (streiche die 6)
19/95 → 1/5 (streiche die 9)
26/65 → 2/5 (streiche die 6)
49/98 → 4/8 = 1/2 (streiche die 9)
Sie werden in der englischen Literatur als digit-cancelling fractions oder anomalous cancelling fractions bezeichnet.
"Euler Problem 33"
| # | a/b | off | c/d | :x |
| 1 | 16/64 | 6 | =1/4 | :16 |
| 2 | 19/95 | 9 | =1/5 | :19 |
| 3 | 26/65 | 6 | =2/5 | :13 |
| 4 | 49/98 | 9 | =1/2 | :49 |
Erweitert man die Suche auf dreistellige Zahlen und verlangt, dass zwei Ziffern gestrichen werden müssen (und nicht mehr als eine Ziffer "0" enthalten ist), entstehen die wirklich verblüffenden Beispiele – wir nennen sie hier die Ästhetischen Fun Fracts.
Beispielsweise:
124/217 → 4/7 (streiche 1+2)
163/326 → 1/2 (streiche 3+6)
316/632 → 1/2 (streiche 3+6)
455/546 → 5/6 (streiche 4+5)
499/998 → 1/2 (streiche 9+9)
Insgesamt fand ich 30 solcher eleganten Fälle im 3-stelligen Bereich:
Non-trivial Anomalous Cancelling Fractions >100
| # | a/b | off | c/d | :x |
| 1 | 124/217 | 1 + 2 | =4/7 | :31 |
| 2 | 127/762 | 2 + 7 | =1/6 | :127 |
| 3 | 138/184 | 1 + 8 | =3/4 | :46 |
| 4 | 139/973 | 3 + 9 | =1/7 | :139 |
| 5 | 145/435 | 4 + 5 | =1/3 | :145 |
| 6 | 148/185 | 1 + 8 | =4/5 | :37 |
| 7 | 160/640 | 0 + 6 | =1/4 | :160 |
| 8 | 163/326 | 3 + 6 | =1/2 | :163 |
| 9 | 166/664 | 6 + 6 | =1/4 | :166 |
| 10 | 182/819 | 1 + 8 | =2/9 | :91 |
| 11 | 187/748 | 7 + 8 | =1/4 | :187 |
| 12 | 190/950 | 9 + 0 | =1/5 | :190 |
| 13 | 199/995 | 9 + 9 | =1/5 | :199 |
| 14 | 218/981 | 1 + 8 | =2/9 | :109 |
| 15 | 244/427 | 2 + 4 | =4/7 | :61 |
| 16 | 260/650 | 0 + 6 | =2/5 | :130 |
| 17 | 266/665 | 6 + 6 | =2/5 | :133 |
| 18 | 273/728 | 2 + 7 | =3/8 | :91 |
| 19 | 316/632 | 3 + 6 | =1/2 | :316 |
| 20 | 327/872 | 2 + 7 | =3/8 | :109 |
| 21 | 364/637 | 3 + 6 | =4/7 | :91 |
| 22 | 412/721 | 1 + 2 | =4/7 | :103 |
| 23 | 424/742 | 2 + 4 | =4/7 | :106 |
| 24 | 436/763 | 3 + 6 | =4/7 | :109 |
| 25 | 448/784 | 4 + 8 | =4/7 | :112 |
| 26 | 455/546 | 4 + 5 | =5/6 | :91 |
| 27 | 484/847 | 4 + 8 | =4/7 | :121 |
| 28 | 490/980 | 9 + 0 | =1/2 | :490 |
| 29 | 499/998 | 9 + 9 | =1/2 | :499 |
| 30 | 545/654 | 5 + 4 | =5/6 | :109 |
Die Literatur (vgl. Boas 1979, sowie Wolfram MathWorld: Anomalous Cancellation) zeigt, dass es im 4-stelligen Bereich sehr viele solcher Brüche gibt – insgesamt 1851. Darunter sind aber viele „triviale“ (etwa nur Nullen gestrichen).
Einige der ersten nicht-trivialen Beispiele (aus MathWorld/Wolfram):
| # | a/b | off | c/d |
| A | 1016/4064 | 6 | =101/404 |
| B | 1019/5095 | 0 + 9 | =11/ 55 |
Sie zeigen, dass das Phänomen nicht auf kleine Zahlen beschränkt ist – aber die wirklich schönen, „menschlich verblüffenden“ Beispiele werden seltener.
L. Boas (1979): Curious Cancelling Fractions
Project Euler Problem 33: Digit Cancelling Fractions
Wolfram MathWorld: Anomalous Cancellation
![]() ©
by
Dr. Hilmar Alquiros,
The Philippines
Impressum Data
Protection Statement / Datenschutzerklärung
©
by
Dr. Hilmar Alquiros,
The Philippines
Impressum Data
Protection Statement / Datenschutzerklärung ![]()
û