dr. hilmar ebert, aachen

Faschingsschach 2000 ...

Sensation: Mensch löst Schachaufgabe 16 mal „schneller“ als Computer!

 Da die Zeit bekanntlich immer schnelllebiger zu werden beliebt, liegt es nahe, auch das Lösen von Schachaufgaben über die radikale Verkürzug der geforderten Zügezahlen zu beschleunigen. Zeitvergeudung, Matt in drei oder noch mehr Zügen zu lösen– dafür gibt es doch Computer!

Hilmar Ebert, Aachen

Tele-Tipp 1.1.2000

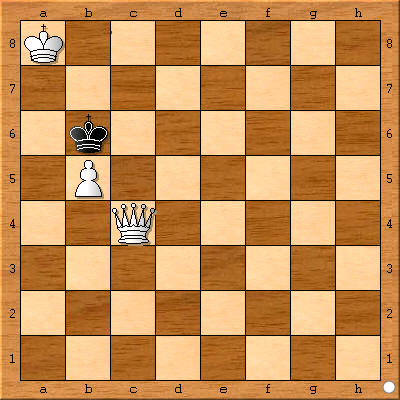
Matt in einem Viertelzug (!!!)

 Computer benötigen hier 4 volle Züge, also das Sechzehnfache der menschlichen Zügezahl, ein schier unüberbietbarer Rekord!?

Computer: Matt in 4! 1.Dd5?/1.Dc7+? Ka5!; 1.Dd4+? (Kb5:?/Kc7?) aber: 1...Ka5! Darum:

1.Kb8!? Ka5  2.Kc8! Kb6  3.Db4 Ka7  4.Da5#  - Na ja, Preisniveau erreicht diese schnöde Lösung sowieso nicht.

Mensch: Matt in ¼! Die wesentlich geistvollere humanoide Lösung! Schwarz hatte natürlich zuletzt a7-a5 gezogen, das dürfen wir (allerdings nur an Fasching und an Silvester!) unterstellen. Der schwarze Bauer a5 wurde bereits entfernt (e.p.-Schlag) = ein halber Zug; der Bauer führt nun von seinem nächsten halben Zug (b5-a6) nur die Hälfte aus, landet also auf dem Schnittpunkt aus a/b und 5/6 = ein Viertelzug, von wo aus er fröhlich mattsetzt, von der Dame sichtlich gedeckt. Überdies ein sogenanntes Idealmatt, da alle Steine am Matt beteiligt sind und jedes Fluchtfeld aus nur einem Grunde verwehrt ist, somit problemschachästhetisch begründet!

P.S.

 In Hilfsmatt-üblicher Zählung (der weiße Mattzug als Teil eines Zugpaares = Halbzug) ist hier bereits das (Hilfs-) Matt in einem Achtelzug erreicht, drum setzt der Autor an dieser Stelle ein Flasche Champagner aus für die erste korrekte Darstellung eines Matt in einem Sechzehntelzug  ...

Herzlichst

h.e.